Matrices

2/12 in Linear Algebra. See all.

Matrices
Matrices are pretty simple. They're just arrays of column vectors. For example, the matrix

is a matrix. The first row is , and the second row is . The first column is , the second column is , and the third column is .

Matrix Equivalency
Two matrices and are equivalent if there exist two real numbers and such that the following conditions hold:

Corresponding indices of and are equivalent.

Matrix Addition
Matrix addition is defined elementwise — add corresponding elements. Matrix addition is commutative () and associative (). Undefined if the orders of and are not the same.

Scalar Multiplication
For a matrix and real number , is defined by .

Matrix Multiplication
Let and be positive integers, be a matrix with order , and be a matrix with order . The product matrix, , is the matrix defined by

For and . This means that is obtained by multiplying the th row of with the th row of and summing. The multiplicative identity matrix is the diagonal matrix with only as its diagonal elements (and is denoted by ).

If and are matrices such that is defined, then . Here's a gif:

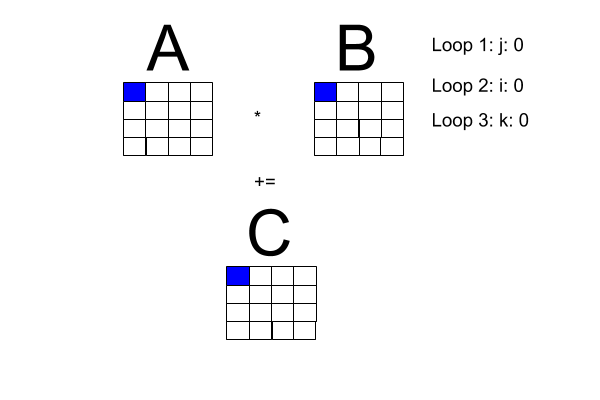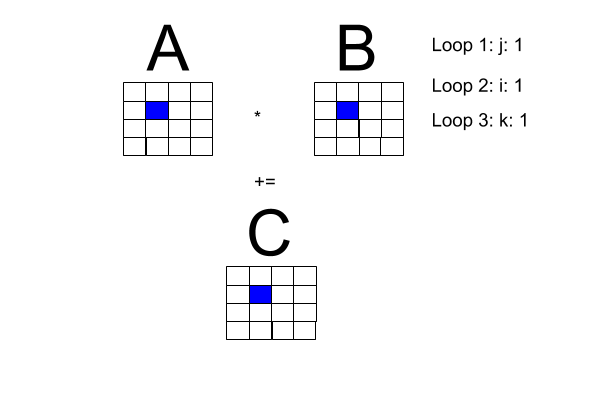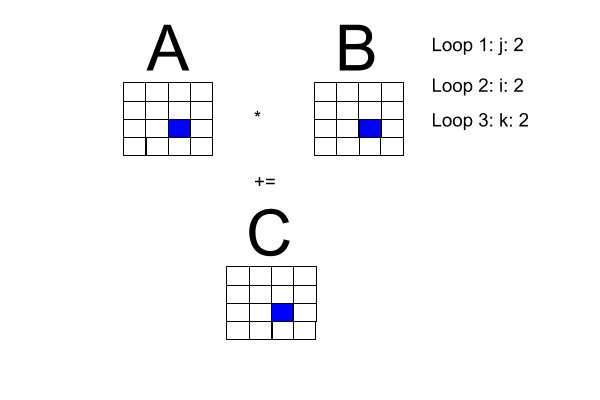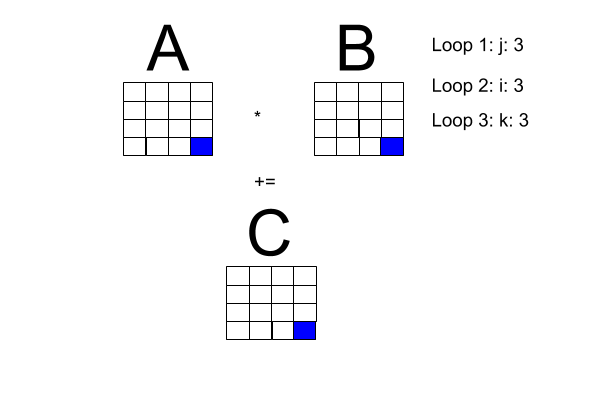
Special Types of Matrices

There are some special types of matrices that we'll need to know about.

Identity Matrix
The identity matrix is a square matrix with 's on the main diagonal and 's elsewhere. It is denoted by (where is the order of the matrix). The identity matrix is the multiplicative identity for matrices: .

Zero Matrix
The unique zero matrix of order is a matrix (of order ) whose entries are all zero. It is denoted with . If and have the same order, then .

Triangular Matrices

Upper Triangular: A square matrix is upper triangular if whenever .
Lower Triangular: A square matrix is lower triangular if whenever .
An upper triangular matrix has elements that are all below the main diagonal, and a lower triangular matrix has zero elements above the main diagonal. The product of a UT or LT matrix with another UT or LT (must be the same) matrix is also UT or LT (must be the same).
Here's an example of an upper triangular matrix:

Diagonal Matrix
A diagonal matrix is a matrix where all the elements are zero except for the diagonal elements. The product of two diagonal matrices is also a diagonal matrix. So, a diagonal matrix is both UT and LT.

Sub-matrix
A sub-matrix of a matrix is any matrix obtained by removing a number of rows or columns from . We'll need this when we talk about the determinant.

Partitioned Matrix
A matrix is partitioned if it is divided into submatrices by horizontal and vertical lines between rows and columns. The resulting submatrices are often called blocks. Matrices are compatibly partitioned if the number of horizontal blocks in the number of vertical blocks in (i.e., the block dimensions are multiplicable) AND each block block operation "makes sense" — i.e., the submatrices can be multiplied.
Note that partitioning a matrix doesn't change anything about the matrix — it's just a way to organize the matrix.

Symmetric Partition
A symmetrically partitioned matrix is one where the horizontal and vertical partition lines occur in the same places relative to the sequence of rows and columns.

Diagonal Block
A diagonal block (in a symmetrically partitioned matrix) can be defined in two ways:

A block bounded by the -th and st horizontal AND vertical partition lines.
A block whose diagonal elements are all diagonal elements of .
Each diagonal block must be square. A block diagonal matrix is one whose nondiagonal blocks are all zero submatrices.

Special Matrix Definitions

Row Equivalence
Two matrices are row equivalent if one can be changed to the other by a sequence of elementary row operations.

Positive Integral Power
(for any positive integer ) is called a "positive integral power of ."

Transpose
The transpose of a matrix is the matrix such that

Essentially, each row of becomes a column of . Transposes have the following properties:

Symmetry
A matrix is symmetric if . This can be possible if and only if is square and . So, the main diagonal can be anything, but the other elements must be symmetric.

Skew Symmetry
A matrix is skew symmetric if . This is true if and only if is square and . A skew symmetric matrix must have all diagonal elements equal to .
It is a good exercise to prove that a skew symmetric matrix squared is symmetric, and is skew symmetric.

Prev: Vectors and Coordinate Spaces Next: Linear Systems of Equations

Back to Linear Algebra